Foi com Pierre de Fermat que se começou a pensar no uso da indução na matemática. Aos meados do século XVII, ele tenta demonstrar que todos os inteiros da forma
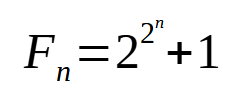
seriam primos, considerado n inteiro e diferente de zero. Ele fez essa conta até n igual a 6 (18.446.744.073.709.551.617) e reputou a todos que eram números primos [MOUTTA, 2013, p. 23]1. O Confronto com essa questão é recorrente até agora.

Fonte: Wikipedia.
Entretanto, Euler chega, em 1743, à conclusão de que já para n igual a 5, a expressão não levava a um número primo, posto que o resultado (4.294.967.297) é divisível por 641. [Ibd. p. 25]
Na esteira de Gauß, a maioria dos autores se utilizam das séries para elucidar os mecanismos operados pela Indução Finita. Já o professor Fábio Henrique de Souza2, privilegia o exemplo da cadeia de dominós, mas também, em diversos vídeos de sua autoria, aplica o Princípio da Indução Finita (PIF) em variadas situações e fenômenos. Nesse aspecto, o ínclito professor carioca, mostra com muita propriedade a diversidade experimental dessas aplicações.
Naturalmente, o emprego dessa importante ferramenta da Matemática Experimental não só é desferida em questões da realidade física, mas, em especial, no ambiente abstrato. No Laboratório Virtual do Jovem Pesquisador realizado em 28.11.20, discutiu-se o PIF num emblema por demais vivenciado por adolescentes: os apaixonamentos. Certamente, a estranheza em face da escolha do objeto da análise revelou-se nítida, mas ao final todos concordaram com a oportunidade ímpar de provocar a atenção e o interesse dos adolescentes para uma ferramenta extremamente complexa e controversa como no caso do PIF.
A título de outros exemplos que poderiam chamar a atenção de adolescentes, num processo de popularização da matemática, foram escolhidos alguns outros fenômenos exóticos: (a) o jogo Sudoku foi objeto de análise, tomando-se como hipótese estratégias de jogo, (b) o fenômeno da eleição no 2.º turno em São Paulo também foi analisado, tomando-se como hipótese a reversão das previsões com fundamento em eventuais pontos favoráveis, (c) o fenômeno natural chuva, quando várias hipóteses foram propostas, mas prevaleceu uso da popularmente conhecidas como nuvens carregadas.

Fonte: Wikipedia.
Sem objeção, a Indução Finita se presta, em particular, para o manuseio e cálculo com os Números Naturais. Nesse sentido, ao estudo da função (injetiva) pertinente à sucessão [ s(n) ] dos integrantes desse conjunto, formalmente se chega à conclusão de que o zero não pertence ao conjunto dos Números Naturais. A certeza, paradoxalmente, advém dos Axiomas de Peano, que demonstram claramente que todos os naturais possuem sucessor e antecessor, salvo o número 1 (um), que não possui antecessor, porquanto o zero (que supostamente antecederia o número 1 na cadeia dos Naturais) não pode participar do conjunto dos Números Naturais, posto não ter sucessor.
Assim, exige-se dos fenômenos (transcendentais, mesmo em forma de incógnita, ou imanentes) a serem analisados pelo PIF, que obrigatoriamente apresentem a capacidade de matematização ao uso de Números Naturais e conveniências aritméticas na espécie.
A pobreza em credibilidade da Indução Finita na Matemática não se deve a falha argumentativa ou eventual inconstâncias dos fundamentos justapostos. Esse método é largamente utilizado e prestigiado nas inúmeras ciências experimentais; a diferença é que, na Matemática, esse instrumento é usado fortuitamente. Com uso mais frequente e alargado do PIF, certamente a devida precisão e credibilidade exsurgiriam.
Projeto Jovem Pesquisadores
Inscrições: https://forms.gle/EPa8rajipnHkNy7i7
Informações: academiacearensedematematica@gmail.com
1MOUTTA, Welbert de Oliveira: A introdução do Princípio da Indução Finita nos Ensinos Fundamental e Médio. Dissertação de Mestrado. (Orientador: Roberto Imbuzeiro Oliveira). Rio de Janeiro: IMPA, 2013.
2Fonte: https://www.youtube.com/watch?v=bhfhmre-QxU&list=PLrVGp617x0hAb3bokPETMb7ymiVW_FtuM

