Equações Diferenciais Ordinárias

Inscrições: https://forms.gle/Sunh772XxCKq6Fz1A

Informações: acm@acm-itea.org

Provavelmente, a melhor e bem mais completa definição de Equações Diferenciais, só será encontrada em Rainville et Bedient (1997, p.1), conforme se toma abaixo (em tradução livre):

“A construção de modelos matemáticos para aproximar problemas do mundo real tem sido um dos aspectos mais importantes do desenvolvimento teórico de cada um dos ramos da ciência. Muitas vezes, esses modelos matemáticos envolvem uma equação na qual uma função e suas derivadas desempenham papéis importantes.

Tais equações são chamadas de equações diferenciais. Como na equação (3), uma derivada pode estar envolvida implicitamente pela presença de diferenciais. Nosso objetivo é encontrar métodos para resolver equações diferenciais; isto é, encontrar a função desconhecida ou funções que satisfaçam a equação diferencial.”

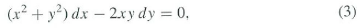
Essa orientação dos autores em questão para a vertente da realidade, é justamente o objetivo do Prof. Rodney Carlos Bassanezi na presente palestra; inclusive entrevendo a “solução para evitar epidemias, guerras e outras catástrofes provocadas pelo excesso de população …”

Em duas etapas vai evoluir a palestra.

Na primeira abordagem, a Modelagem Matemática exsurge como veículo de abordagem dos problemas da dinâmica populacional e suas consequências, sem menosprezar a iteração de populações.

O princípio da Extensão de Zadeh e o Modelo malthusiano Fuzzi tomarão importante representação nas abstrações e trabalhos matemáticos da averiguação.

No segundo momento da palestra, o manejo da Covid-19 por Equações Diferenciais, mesmo quando submetido a Modelos Compartimentais. Em especial, trata do Modelo de Manaus, talvez a situação mais grave enfrentada no Brasil.

Referência

RAINVILLE, E. D.; BEDIENT, P. E. Elementary differential equations. 8th. ed. Saddle River, NJ: Prentice-Hall, Inc., 1997.

Rodney Carlos Bassanezi

Possui graduação em Matemática pela Universidade Estadual Paulista Júlio de Mesquita Filho (1965), mestrado em pela Universidade Estadual de Campinas (1971) e doutorado em Matemática pela Universidade Estadual de Campinas (1977).

Trabalhou no IMECC- Unicamp de 1969 a 2001 quando passou a ser pesquisador voluntário nesta universidade, permanecendo até 2006.

A partir de 2007 trabalha na Universidade Federal do ABC onde foi o primeiro coordenador do programa de pós-graduação do CMCC.

Tem experiência na área de Matemática, com ênfase em Análise, atuando principalmente nos seguintes temas: Teoria Fuzzy; Sistemas dinâmicos subjetivos; Biomatematica (epidemiologia), ecologia ; Educacao matematica (Modelagem).