Sistemas Variacionais p-Fuzzy

Inscrições: https://forms.gle/KwVBTreo6T2CjJxHA

Informações: acm@acm-itea.org

Uma profunda reflexão exige-se ao que o eminente mestre Rodney Bassanezi leciona, in verbis:

A maior dificuldade que notamos para a adoção do processo de modelagem, pela maioria dos professores de matemática, é a transposição da barreira naturalmente criada pelo ensino tradicional onde o objeto de estudo apresenta-se quase sempre bem delineado, obedecendo a uma sequência de pré-requisitos e que vislumbra um horizonte claro de chegada – tal horizonte é muitas vezes o cumprimento do programa da disciplina.

(BASSANEZI, 2012)

O renomado mestre ainda enfatiza:

Na modelagem, o início é apenas o tema de estudo escolhido onde ainda não se tem idéia do conteúdo matemático que será utilizado. Nesse estágio, colocamos para os iniciantes que quando não se tem nenhuma ideia do que fazer, comece “contando” ou “medindo” – com este procedimento, é natural aparecer uma tabela de dados e isto pode ser o começo da modelagem.
A disposição dos dados em um sistema cartesiano e um bom ajuste dos seus valores, facilitará a visualização do fenômeno em estudo, propiciando tentativas de propostas de problemas, conjecturas ou leis de formação.
A formulação de modelos matemáticos é simplesmente uma consequência deste processo.
A situação colocada desta forma pode dar a falsa impressão que aprender modelagem matemática é como aprender o conteúdo de uma disciplina bem estruturada. Entretanto, o aprendizado de modelagem não se restringe ao aprendizado de técnicas padronizadas ou procedimentos sequenciais tal como um protocolo cirúrgico. Da mesma forma que só se pode aprender a jogar futebol, jogando, só se aprende modelagem, modelando! O técnico pode aprimorar o comportamento de um jogador e ensaiar jogadas mais efetivas mas o resultado final depende exclusivamente da criatividade e habilidade deste jogador; ainda assim, em cada partida sua atuação e rendimento podem ser bastante diferenciados, dependendo do comportamento da equipe adversária.
O mesmo se dá em todas as atividades que exigem alguma dose de criatividade – a pintura é um exemplo típico: o indivíduo pode aprender todas as técnicas de uma pintura e saber misturar todas as cores, pode inclusive reproduzir alguma obra de outro pintor mas não será um bom artista se não aliar uma boa dose de criatividade às suas habilidades técnicas. (Ibid.)

Daí, Bassanezi conclui:

A atividade de aplicar matemática é tão antiga quanto à própria matemática. É sabido que muitas ideias em matemática surgiram a partir de problemas práticos. Também é verdade que o uso de matemática em outras áreas do conhecimento tem crescido substancialmente a ponto de se esperar que ela venha a resolver todos os tipos de situações. Apesar disso, por mais que se treine um matemático com o estudo de teorias, é evidente que grande parte deles não demonstre habilidades para empregar matemática em outras áreas. O que entendemos por habilidades neste contexto, consiste em tomar um problema definido em alguma situação prática relativamente complexa, transformá-lo em um modelo matemático e procurar uma solução que possa ser reinterpretada em termos da situação original. (Ibid.)

Todo esforço na matematização da realidade abstrata perpassa ao quê

A modelagem matemática é simplesmente uma estratégia utilizada para obtermos alguma explicação ou entendimento dessas situações reais. No processo de reflexão sobre a porção da realidade, você irá selecionar os argumentos considerados essenciais e procurará uma formalização artificial (modelo matemático) que contemple as relações que envolvem tais argumentos. (BERTONE; BASSANEZI; JAFELICE, 2014)

As propriedades do chamado Sistema Fuzzy vão oferecer grandes oportunidades para a matematização de situações da realidade com maior carga de abstração ou subjetividade, conforme desenlaça Ricardo Tanscheit (TANSCHEIT, [s.d.])⁠ na seguinte obervação:

Seres humanos são capazes de lidar com processos bastante complexos, baseados em informações imprecisas ou aproximadas. A estratégia adotada pelos operadores humanos é também de natureza imprecisa e geralmente possível de ser expressa em termos linguísticos. A Teoria de Conjuntos Fuzzy e os Conceitos de Lógica Fuzzy podem ser utilizados para traduzir em termos matemáticos a informação imprecisa expressa por um conjunto de regras linguísticas. Se um operador humano for capaz de articular sua estratégia de ação como um conjunto de regras da forma se … então, um algoritmo passível de ser implementado em computador pode ser construído. O resultado é um sistema de inferência baseado em regras, no qual a Teoria de Conjuntos Fuzzy e Lógica Fuzzy fornecem o ferramental matemático para se lidar com as tais regras linguísticas.

Mais adiante o mesmo autor lembra que

O objetivo aqui é introduzir os conceitos fundamentais da Teoria de Conjuntos Fuzzy, da Lógica Fuzzy e de Sistemas de Inferências Fuzzy, de modo a permitir um contato inicial com este campo extremamente vasto, com aplicações nas mais diferentes áreas do conhecimento. As primeiras aplicações bem sucedidas situaram-se na área de Controle, mas, desde então, tem-se verificado uma utilização crescente de sistemas fuzzy em outros campos, como, por exemplo, classificação, previsão de séries, mineração de dados, planejamento e otimização. O uso conjunto da lógica fuzzy e de outros sistemas classificados como inteligentes – redes neurais e programação evolutiva, por exemplo – tem propiciado a construção de sistemas híbridos, cuja capacidade de aprendizado tem ampliado o campo de aplicações. [Ibid.]

Na mesma linha, vai deslindar argumentação similar (SILVA; BASSANEZI, 2006)⁠:

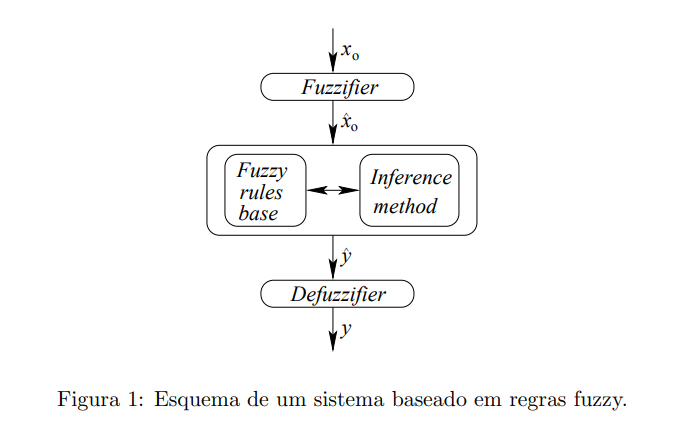
Sistemas baseados em regras fuzzy têm sido utilizados com êxito em várias áreas como controle, para tomadas de decisões, sistemas de identificação, etc. Este sucesso se deve principalmente à sua simplicidade, intuitividade e principalmente a sua inter-relação com a forma de raciocínio humano. Sistemas baseados em regras fuzzy são conceitualmente simples (Fullér, 1995). Tais sistemas consistem basicamente de três estágios (Figura 1): um estágio de entrada-fuzificador, um estágio de processamento, composto por uma base de regras fuzzy e um método de inferência e um estágio de saída – defuzificador.

Assim, podemos tomar que, na visão de SILVA (2005)⁠:

Um sistema dinâmico p-fuzzy é um sistema cuja dinâmica é obtida através de um sistema baseado em regras fuzzy. Neste trabalho, realizamos um estudo analítico da estabilidade dos sistemas dinâmicos p-fuzzy. Estabelecemos condições necessárias e suficientes para existência de ponto de equilíbrio para sistemas p-fuzzy unidimensionais e bidimensionais e derivamos condições para estabilidade deste ponto. Vimos que, uma condição suficiente para existência de ponto de equilíbrio é uma mudança de sinal na saída do controlador. Este trabalho mostra ainda, que a estabilidade de um ponto de equilíbrio depende, principalmente, das variáveis de entradas e saídas do sistema baseado em regras fuzzy associado ao sistema p-fuzzy. Além dos diversos resultados matemáticos encontrados, com demonstrações rigorosas, realizamos inúmeros experimentos computacionais e obtivemos resultados que atestam a veracidade da teoria aqui proposta. Apresentamos ainda, algumas aplicações em Biomatemática onde podemos comprovar, em situações concretas, a eficácia, versatilidade e robustez da teoria desenvolvida.

Referências

BASSANEZI, R. C. Temas & Modelos. Autor ed. Campinas – SP: UFABC, 2012.
BERTONE, A. M. A.; BASSANEZI, R. C.; JAFELICE, R. S. DA M. Modelagem Matemática. Uberlândia- MG: UFU, 2014.
SILVA, J. DE D. M. DA. Análise de Estabilidade de Sistemas Dinâmicos P-fuzzy com Aplicações em Biomatemática. Campinas – SP: IMECC, 2005.
SILVA, J. DE D. M. DA; BASSANEZI, R. C. Pontos Estacionários: I. Sistemas Dinâmicos P-fuzzy Unidimensionais. Disponível em: http://www.ime.unicamp.br/~biomat/bio16_art6.pdf. Acesso em: 1 ago. 2022.
TANSCHEIT, R. SISTEMAS FUZZY. [s.d.].

Rodney Carlos Bassanezi

Possui graduação em Matemática pela Universidade Estadual Paulista Júlio de Mesquita Filho (1965), mestrado em pela Universidade Estadual de Campinas (1971) e doutorado em Matemática pela Universidade Estadual de Campinas (1977).

Trabalhou no IMECC- Unicamp de 1969 a 2001 quando passou a ser pesquisador voluntário nesta universidade, permanecendo até 2006.

A partir de 2007 trabalha na Universidade Federal do ABC onde foi o primeiro coordenador do programa de pós-graduação do CMCC.

Tem experiência na área de Matemática, com ênfase em Análise, atuando principalmente nos seguintes temas: Teoria Fuzzy; Sistemas dinâmicos subjetivos; Biomatemática (epidemiologia), ecologia ; Educacao Matemática (Modelagem).