
Nathan de Souza
Graduando em Matemática Bacharelado pela Universidade Federal do Ceará – UFC. Jovem Pesquisador na Academia Cearense de Matemática – ACM. Menção Honrosa (2016) – Olimpíada Brasileira de Matemática das Escolas Públicas (OBMEP), Instituto de Matemática Pura e Aplicada – IMPA. Menção Honrosa (2017) – Olimpíada Brasileira de Matemática das Escolas Públicas (OBMEP), Instituto de Matemática Pura e Aplicada – IMPA. Medalha de Bronze (2018) – Olimpíada Brasileira de Matemática das Escolas Públicas (OBMEP), Instituto de Matemática Pura e Aplicada – IMPA. Medalha de Ouro (2018) – Olimpíada Brasileira de Astronomia (OBA), Sociedade Brasileira de Astronomia – SAB. Destaque Jovem Pesquisador’2019, pela Academia Cearense de Matemática-ACM. Homenagem (2019) da Assembleia Legislativa do Estado do Ceará – ALCE.
“A arte de fazer matemática consiste em achar aquele caso especial no qual haja todos os germes de generalidade.”
David Hillbert (1862-1943), Mathematical Maxims and Minims, de Nicholas J. Rose. Raleigh (EUA): Rome Press, 1988.
O que David Hillbert disse é o que sintetiza com muita precisão grande parte das descobertas matemáticas. Muitas das vezes, grandes áreas e conhecimentos matemáticos surgem quando você se prende à um problema específico e, após resolvê-lo, uma ideia geral baseada nesta solução, assoma.
Hillbert foi um matemático alemão de grande prestígio e possui até axiomas que levam seu nome, entretanto, o prestigiado deste texto é outro matemático: Leonhard Euler (1707 – 1783). Na cidade de Königsberg (hoje Kaliningrado), onde Hillbert nasceu, Euler resolvera um problema muito famoso acerca das pontes da cidade. Um rio corta a cidade em quatro massas de terra conectadas por sete pontes. O problema era: é possível passar por todas as pontes sem repetir nenhuma?
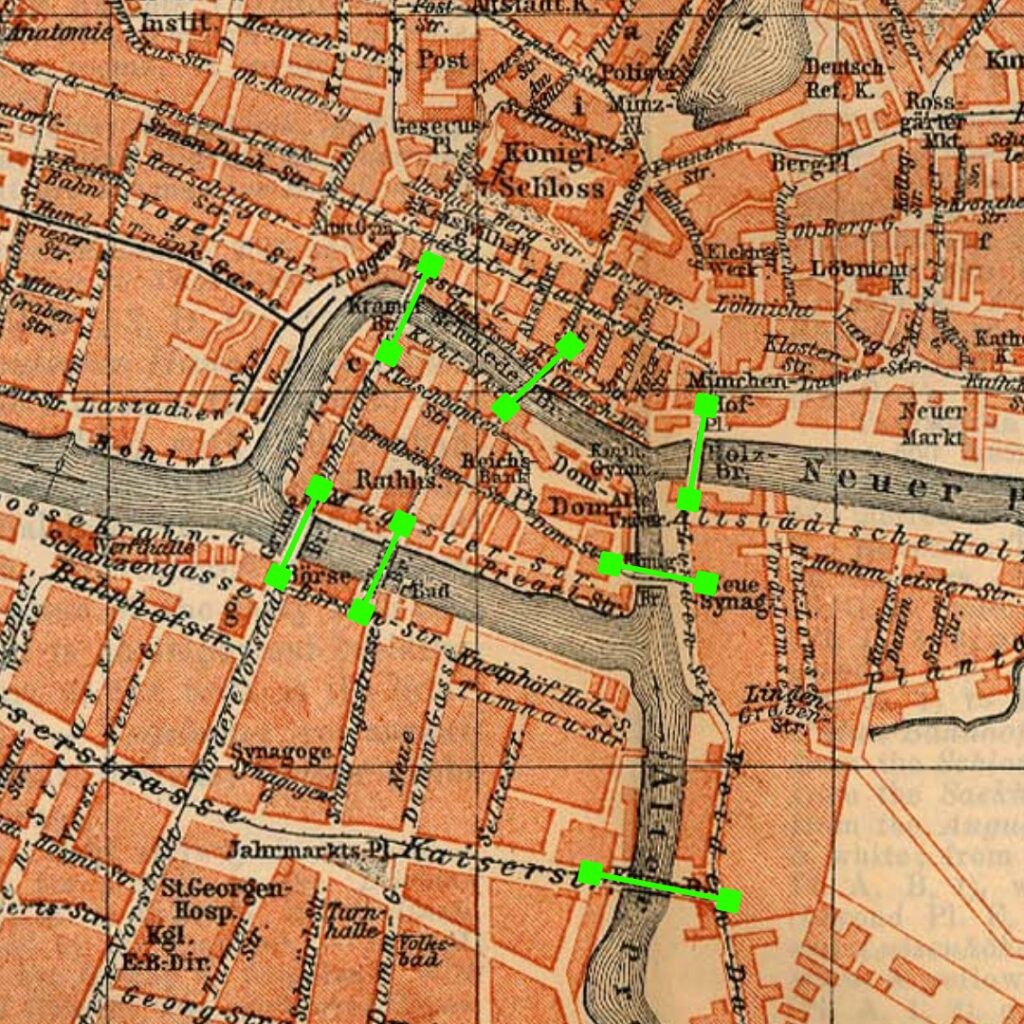
Euler foi um matemático de currículo extenso, deu incontáveis contribuições em outros incontáveis ramos da matemática. Em Königsberg, Euler tomou conhecimento do problema das sete pontes e após pensar e desenhar alguns diagramas, resolveu o problema.

Mas o quê tem de tão especial nisso? Ao resolver o problema, para facilitar a visualização, Euler simplificou o problema com um diagrama bem diferente. Ele transformou as quatro massas de terra em pontos e as pontes em linhas que conectavam esses pontos.

Depois de fazer este diagrama, Euler se deu conta de um fato e resolveu o problema: não é possível passar por todas as pontes sem repetir nenhuma! Sem entrar nas ponderações do problema, o que de fato importa é o diagrama, que é considerado o primeiro resultado na Teoria dos Grafos.
Grafos, sobretudo, nos ajudam a visualizar dados e as relações entre estes dados. No caso de Euler, os dados eram as massas de terra e as relações eram as pontes, mas é possível montar este mesmo esquema para qualquer outra coisa: pessoas e as relações de amizade entre elas em uma rede social; relação entre números; cálculos de percursos, dentre outras inúmeras aplicações.
Grafos, em essência, são tabelas que informam objetos e quais as relações entre esses objetos. Os pontos e linhas servem exatamente para visualizar e verificar possíveis meios para resolver um determinado problema. É um excelente exemplo de casos particulares que nos ajudam a generalizar ferramentas para solução de problemas.

