Inscrições: https://forms.gle/2jZQZuJcEvVbYsKb7
Informações: acm@acm-itea.org
A presente palestra terá início com um breve panorama histórico acerca do estudo das curvas ao longo do século XVII. Serão apresentados os conceitos de curvas geométricas e não geométricas, abordando-se as diferenças conceituais dessas ao longo dos anos e as dificuldades enfrentadas pelos matemáticos da época ao lidarem com curvas transcendentais, especialmente em função da ausência de uma simbologia adequada para representá-las.
Na sequência, serão discutidos os chamados problemas da tangente inversa, sua estreita relação com o desenvolvimento do cálculo infinitesimal, bem como a persistência de métodos geométricos utilizados por alguns geômetras, a exemplo de Christiaan Huygens (1629-1695), que demonstrava preferência por abordagens de natureza construtiva e visual.
A exposição prosseguirá com a análise de propriedades da Tractriz, tal como tratadas por Huygens, em uma de suas correspondências endereçadas a H. Basnage de Beauval (1656-1710). Dentre essas propriedades, destacam-se: a possibilidade de mensuração do comprimento da curva utilizando a própria Tractriz e procedimentos geométricos; a proporcionalidade existente entre tal comprimento e segmentos determinados sobre o eixo das ordenadas; e, por fim, a aplicação da Tractriz no cálculo de áreas delimitadas por uma hipérbole.
A palestra será concluída com uma reflexão sobre a predominância do pensamento geométrico entre alguns matemáticos europeus do período, mesmo diante do crescente interesse por abordagens algébricas e pela introdução do cálculo infinitesimal como ferramenta analítica.
1. Evolução Histórica da Tractriz
A Tractriz, também conhecida como curva de perseguição, tem suas origens no século XVII. Ela foi primeiramente descrita por Claude Perrault em 1670, em um contexto de estudos sobre mecânica e movimento (BOYER, 1991). Poucos anos depois, Christiaan Huygens explorou suas propriedades geométricas, dando impulso ao interesse da comunidade matemática. A curva também apareceu nas investigações de Gottfried Wilhelm Leibniz e Isaac Newton, que procuravam relações entre movimento e geometria.
Com o advento do cálculo diferencial, a Tractriz ganhou um novo patamar de análise. Leibniz e Johann Bernoulli a estudaram como exemplo paradigmático de curva gerada por condições dinâmicas (BOYER, 1991). Já no século XVIII, os estudos sobre catenárias e linhas de força a colocaram em evidência nos trabalhos de Euler. Posteriormente, no século XIX, foi incorporada ao arcabouço das curvas transcendentais estudadas pela escola alemã de matemática (GRAY, 2008).
Durante o século XX, a Tractriz voltou à cena com o surgimento da matemática aplicada e da modelagem. Ela apareceu em estudos sobre cabos de navios rebocados e em modelos biomecânicos de tendões (THOMAS & FINNEY, 2005). A digitalização de curvas e seu uso em design também ampliaram seu papel no ensino e na engenharia. Assim, sua evolução reflete a intersecção contínua entre intuição geométrica, ferramentas matemáticas e aplicação prática.
2. Perspectivas Científicas sobre a Tractriz
Do ponto de vista matemático, a Tractriz é definida como a curva traçada por um ponto sendo puxado por outro ao longo de uma linha reta, com uma corda de comprimento constante. Sua equação diferencial é dada por
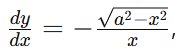
sendo a o comprimento da corda (COURANT & ROBBINS, 1996). Esse modelo permite uma visualização rica do conceito de função implícita e de soluções de equações diferenciais ordinárias. A curva também é importante para ilustrar fenômenos assintóticos, pois ela se aproxima do eixo x sem nunca tocá-lo.
Na Física, a Tractriz surge como modelo em problemas de resistência e tração. Ela descreve, por exemplo, o caminho seguido por um barco sendo rebocado por outro em linha reta (FORSYTH, 1890). Além disso, serve como base teórica para estudos de atrito e movimento com restrições. Isso a torna relevante para diversas engenharias, especialmente mecânica e naval.
A Tractriz também encontra lugar na Computação Gráfica e em Robótica. Algoritmos de rastreamento e simulação de movimentos com vínculos rígidos fazem uso de sua formulação (STROUD & BOOTH, 2011). Em robôs de reboque, por exemplo, ela é empregada para modelar o trajeto de um robô secundário seguindo outro. Sua presença nesses campos destaca sua versatilidade como ferramenta de modelagem matemática.
3. Enfoques Experimentais e Projetos Didáticos
A experimentação com a Tractriz pode começar com uma simples simulação física utilizando cordões e objetos deslizantes. Essa abordagem permite aos alunos observarem a curva emergente e explorarem hipóteses sobre seu comportamento. Experimentações como essas fomentam o raciocínio investigativo e o pensamento geométrico (PONTE, 2005). Assim, a curva serve como elo entre o concreto e o abstrato no processo de ensino-aprendizagem.
No contexto da modelagem matemática escolar, a Tractriz pode ser explorada com softwares como GeoGebra. A construção dinâmica da curva permite uma análise em tempo real de seus parâmetros (BORBA & VILLARREAL, 2005). Além disso, pode-se propor projetos interdisciplinares envolvendo Física, como o estudo do movimento de corpos ligados por cordas. Tais experiências proporcionam um aprendizado significativo e contextualizado.
A Tractriz também pode ser usada em projetos interativos com Arduino ou robôs educacionais. Um exemplo envolve programar um robô para seguir uma trajetória determinada por uma corda fixa a outro robô. Isso possibilita uma abordagem prática e contemporânea, aproximando a Matemática da Tecnologia (VALENTE, 1999). Projetos assim despertam o interesse e o engajamento dos alunos nas ciências exatas.
4. Relevância Educacional da Tractriz na Educação Básica
A Tractriz oferece oportunidades valiosas para a introdução de conceitos avançados de forma acessível. Ela permite que estudantes explorem noções de geometria diferencial, função e modelagem, mesmo antes do estudo formal do cálculo (D’AMBROSIO, 2001). Assim, ela pode ser utilizada como ponto de partida para investigações investigativas e contextualizadas. Sua inclusão no currículo enriquece o repertório de estratégias pedagógicas.
No Ensino Médio, a Tractriz pode servir como elo integrador entre diversas disciplinas. A Física e a Matemática encontram-se ao explorar sua aplicação em fenômenos reais. Além disso, os conceitos de limite, derivada e integral podem ser abordados de maneira intuitiva. Isso contribui para o desenvolvimento do pensamento lógico-matemático e da interdisciplinaridade.
Sua relevância também está em promover a História da Matemática em sala de aula. Apresentar aos alunos a trajetória de pensadores como Huygens e Bernoulli estimula o pensamento crítico e o reconhecimento da Matemática como construção humana (FURTADO, 2006). Ao entender como uma curva como a Tractriz foi descoberta e usada, os estudantes valorizam o papel da investigação histórica na ciência. Isso favorece uma visão mais ampla e humana do conhecimento.
5. Exemplos de Aplicações e Projetos com a Tractriz
- Simulação de Reboque com Carrinhos: Projeto em que alunos constroem carrinhos ligados por barbantes para observar e registrar a trajetória do segundo carrinho. A atividade permite que os estudantes comparem os dados experimentais com a curva teórica da Tractriz.
- Modelagem Matemática no GeoGebra: Construção da Tractriz com uso de ferramentas digitais para análise da equação diferencial envolvida. Os alunos podem variar parâmetros e observar como o comportamento da curva muda.
- Construção de uma Tractriz com Arduino: Uso de sensores e motores para simular o movimento de dois pontos ligados por uma corda, com geração digital da curva percorrida. O projeto desenvolve habilidades em robótica e programação.
- Estudo Interdisciplinar de Reboque de Navios: Pesquisa e simulação do uso da Tractriz em operações marítimas, com apoio de vídeos e softwares de navegação. O projeto envolve conhecimentos de Física, Geometria e História.
- Análise da Tractriz em Biomecânica: Pesquisa sobre o uso da Tractriz como modelo do movimento de tendões ou músculos em anatomia funcional. Estudantes de áreas técnicas podem integrar Biologia e Matemática nesse estudo.
Referências Bibliográficas (ABNT)
BORBA, Marcelo C.; VILLARREAL, Maria E. Experimentação e Modelagem em Matemática com uso das Tecnologias Digitais. Belo Horizonte: Autêntica, 2005.
BOYER, Carl B. História da Matemática. 2. ed. São Paulo: Edgard Blücher, 1991.
COURANT, Richard; ROBBINS, Herbert. What is Mathematics? An Elementary Approach to Ideas and Methods. New York: Oxford University Press, 1996.
D’AMBROSIO, Ubiratan. Educação Matemática: Da teoria à prática. Campinas: Papirus, 2001.
FORSYTH, Andrew R. A Treatise on Differential Equations. Cambridge: Cambridge University Press, 1890.
FURTADO, Elizabeth. A História da Matemática na Formação de Professores: possibilidades e limites. São Paulo: Livraria da Física, 2006.
GRAY, Jeremy. Plato’s Ghost: The Modernist Transformation of Mathematics. Princeton: Princeton University Press, 2008.
PONTE, João P. da. Investigar para aprender Matemática. In: GTI – Grupo de Trabalho de Investigação. Lisboa: APM, 2005.
PONTES, Acelino. Prolegômenos à Nova Matemática. Fortaleza: Scientia Publishers, 2023. 232 p.
STROUD, K. A.; BOOTH, Dexter J. Engineering Mathematics. 7. ed. London: Palgrave Macmillan, 2011.
THOMAS, George B.; FINNEY, Ross L. Cálculo, Volume 1. 11. ed. São Paulo: Addison Wesley, 2005.
VALENTE, José Armando. O Computador na Sociedade do Conhecimento: repensando a educação. Campinas: UNICAMP/NIED, 1999.
Nota: Parte do texto foi produzida em sinergia com IA.

Gabriel Faria Vieira
Possui graduação em Matemática pela Universidade Federal do Triângulo Mineiro (2021) e mestrado em EDUCAÇÃO EM CIÊNCIAS E MATEMÁTICA pela Universidade Federal do Triângulo Mineiro (2024).
Atualmente é professor de educação básica da Escola Estadual Carmelita Carvalho Garcia.
Tem experiência na área de Matemática, com ênfase em Matemática, atuando principalmente nos seguintes temas: história da matemática, história do cálculo, tractriz, cálculo infinitesimal e matemática.
CV Lattes: http://lattes.cnpq.br/8316885136414563
Comentários
| Muito obrigado pela excelente palestra (Abel do Rosário Sarmento) |
| Contribuiu muito em conhecimento. (Aguinaldo Antonio Rodrigues) |
| Excelente palestra (Carlos Magno de Moraes) |
| Parabéns pelo tema e pela excelente exposição. Parabéns! (Flávio Maximiano da Silva Rocha) |
| Parabéns, excelente palestra, estou aprendendo muito, obrigado por compartilhar o conhecimento. Parabéns! (Hailton David Lemos) |
| Maravilhosa palestra! Muito obrigada pela oportunidade de participar! (Irla Leite de Souza) |
| Excelente tema e apresentação (Ivanildo da Cunha Ximenes) |
| Muito interessante esse trabalho. Parabéns professor Gabriel (Jaqueline de Assis Carvalho) |
| Excepcional essa apresentação, utilizando o Geogebra. (Jefte Dodth Telles Monteiro) |
| Excelente palestra! (Lineu da Costa Araújo Neto) |
| Parabéns professor Gabriel pela palestra. (Lucia dos Santos Bezerra de Farias) |
| Excelente palestra (Luiz José da Silva) |
| Conteúdo de Matemática Pura (Marcos Lengrub da Silva) |
| Ótima palestra (Maria Thalita Abreu Pereira) |
| Excelente Palestra! Sem palavras, muitos elogios! Parabéns Prof. Gabriel! (Maxwell Gonçalves Araújo) |
| Gratidão! (Paulo Sérgio de Andrade Moraes) |
| Ótima palestra. Explicações bem claras. (Ricardo de Carvalho Oliveira) |
| Excelente palestra, muito obrigada, grande contribuição, sempre é bom ter formação continuada, nos engrandece muito. (Suelen Ferreira de Freitas) |
| Maravilhosa palestra (Wanderlania Sousa Alves) |

