No Laboratório Virtual realizado em 21.11.20, a preocupação esteve ligada à afirmação que “uma matemática consistente é uma matemática livre de contradições”. No esteio dessa premissa realizou-se uma abordagem metamatemática do Pi (π) e do Plano Cartesiano, duas ferramentas extremamente importantes no ambiente da Análise Matemática. Com isso, as exigências ao sistema lógico matemático assume uma importância fundante, para esclarecer eventuais contradições e imprecisões.

Naturalmente, a questão da precisão na Matemática não se deixa esclarecer com muita leveza, sem que se utilize de recursos metafísicos e metamatemáticos, em alcançar uma completude analítica, na abordagem. Essa questão foi apreciada com profundidade, em especial e sobretudo ante a consciência da necessidade que assiste à Matemática que seja a mais eficiente e poderosa ferramenta para descrever e mensurar o caos, de que necessita a realidade para existir e se desenvolver. A título de exemplo, tome-se o cérebro humano, um fenômeno de uma densidade caótica extraordinária, mas que se tem descrito com muita eficiência ao uso de ferramentas matemáticas, elucidando grande parte dos enigmas tanto os morfológicos, os fisiológicos, como os funcionais. E essa evolução permite hoje, que uma pessoa sobreviva ao aneurisma cerebral, quando esse diagnóstico, até pouco tempo, fatalmente levaria à morte.
Esses conflitos, se devem, como Stephen Cole Kleene relata com muita propriedade, a uma crise urdida pela teoria dos conjuntos, pela aritmetização da análise e o enfrentamento de uma nova era engendrada por Russell, Whitehead, Hilbert e Brouwer.
Pi (π)
O número do círculo, também conhecido como número de Ludolph ou constante de Arquimedes, é definido como a razão entre o perímetro de uma circunferência e seu diâmetro. Essa proporção independe do tamanho do círculo e ocorre em inúmeras subáreas da matemática, mesmo fora da geometria; frequentemente indicado com apenas dois dígitos aproximados: 3,14. A divisão revela que o perímetro do círculo possui 3 partes inteiras iguais, acrescidas de um pedacinho, que vai fazer toda a diferença: o Pi.

Essa talvez seja a ferramenta mais utiliza no cálculo e na análise matemática, embora apresente um grau de imprecisão extremamente complexo. Entretanto, o Acadêmico Acelino Pontes, coordenador do Laboratório, descreve como no mínimo imprópria, a classificação do Pi como número irracional. Na sua opinião, “a Metamatemática não permite a classificação de número, enquanto entes matemáticos, com a característica de irracional”. Na sua fundamentação, Pontes remete ao que Leibniz (1646-1716) já descrevia como rationem transcendunt (do latim, além da razão), e que Euler (1707-1783) reconhece como quantitas transcendens (quantidade transcendente). Nenhum dos dois vai preconizar a incapacidade de encontrar um quociente preciso, uma ‘irracionalidade’. Aqui temos um conflito do conceito ‘divisão’ com o de ‘razão’. Alhanar razão (argumento lógico) Ao cálculo de um quociente (argumento aritmético) é no mínimo, temerário. Isso, embora questão puramente linguística, ainda não foi bem esclarecida.
Seguindo a imaginação de Arquimedes (287 – 212 a.C.) ao uso do método da exaustão, aplicando polígonos regulares inscrito e outro circunscrito a um mesmo círculo, tenta-se aproximar os polígonos ao desenho da circunferência em questão. Mesmo manipulando ferramentas algébricas e considerando o experimento de Arquimedes com polígonos de 96 lados, não foi possível chegar a construção dos 3 objetos numa só identidade.
Daí, se discute a existência da precisão na Matemática e sua aplicabilidade. A perspectiva da precisão num ambiente abstrato é no mínimo, complexa; sua essência, dificilmente se deixa precisar por métricas quaisquer. Também há de constatar-se que, mesmo as ciências objetivadoras das aplicações matemáticas, não conseguem a precisão absoluta, porquanto se contentam com o cálculo de limites, à sorte de espaços e equações.
Plano Cartesiano
O adjetivo cartesiano faz referência ao matemático e filósofo francês René Descartes (1596-1650), que em busca de uma melhor sistematização de seu método, publicou esse significativo contructo em 1637. De forma independente seus compatriotas Pierre de Fermat (1601 – 1665) e Nicole d’Oresme (1323 -1382), também trabalharam em três dimensões.
Na discussão do Plano Cartesiana há de se constatar a necessidade de esclarecer aos alunos e estudantes, que não se trata de uma questão objetiva, mas tão somente metodológica. Toda a configuração do sistema cartesiano é uma construção metódica, ritualística e fruto de convenções específicas. Assim, a título de exemplo o – ∞ ou + ∞ configurados no sistema para cada um dos incontáveis planos ou espaços possíveis (à direita e à esquerda, para cima e para baixo), objetivamente não implica na existência de incontáveis –∞ e/ou + ∞. Todas as referências, obrigatoriamente, necessitam ser compreendidas como convenções com o intuito de facilitar possíveis cálculos e demonstrações algébricas ou pictóricas. Infelizmente, essa constatação raramente são postuladas em sala de aula.
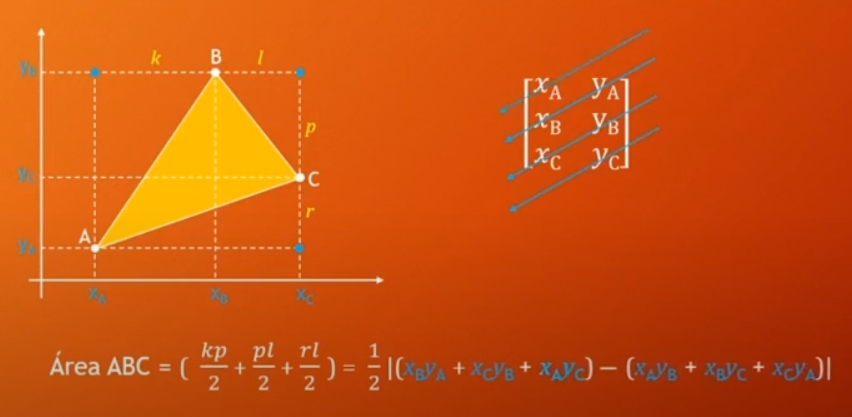
Essa postura ficou muito bem demonstrada com a apresentação de vídeos de autoria do professor Fábio Henrique de Souza, que, ao rigor metamatemático, se utiliza do Plano Cartesiano e também de ferramentas matriciais para análise de objetos escrupulosamente abstratos. Em determinados momentos e construções o professor Fábio Henrique abandona in totum o Plano Cartesiano e produz suas análises e cálculos tão somente no espaço vazio, enriquecendo sobremaneira as suas lições. Essa brilhante metodologia e didática do ilustre lente nos indica que o trabalho matemático é, por excelência, executado no ambiente absolutamente abstrato e ao uso de objetos totalmente abstratos; a manipulação de números e quantidades físicas não promovem um melhor entendimento na espécie, tão somente contraem eventuais indefinições, impurezas e incertezas.
“A análise metamatemática é o melhor engenho para manejar e governar todas as matemáticas, revelando essência, profundidade e beleza”, resume o Acadêmico Acelino Pontes, Coordenador-Geral do projeto Jovem Pesquisador (JP) e presidente da Academia Cearense de Matemática (ACM).

